Prime and Maximal Ideals
Throughout this section, let R be a commutative ring with identity.
Definition 1: Let P be and ideal of R, P  (1). We say that P is a prime ideal if, whenever a,b (1). We say that P is a prime ideal if, whenever a,b  R have the property that ab R have the property that ab  P, then either a P, then either a  P or b P or b  P. P.
Example 1: Let R = Z and let p be prime. Then (p) is a prime ideal. For each ab  (p), then p|ab. Therefore, by Euclid's lemma, p|a or p|b and thus either a (p), then p|ab. Therefore, by Euclid's lemma, p|a or p|b and thus either a  (p) or b (p) or b  (p). (p).
Example 2: Example 1 suggests the following generalization. Let R be a UFD and let  be an irreducible element of R. Then ( be an irreducible element of R. Then ( ) is a prime ideal. The proof is the same as Example 1, except Proposition 5 of the section on factorization in polynomial rings is used rather than Euclid's lemma. ) is a prime ideal. The proof is the same as Example 1, except Proposition 5 of the section on factorization in polynomial rings is used rather than Euclid's lemma.
Example 3: Let R = F[X,Y]. We will prove below that (X,Y) is a prime ideal. (See Corollary 4).
Example 4: Let R = Z. Then (4) is not a prime ideal, since 2 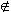 (4), but 2 · 2 (4), but 2 · 2  (4). (4).
Proposition 2: Let R be a principal ideal domain. Then the prime ideals of R are of the form ( ), where ), where  is an irreducible element of R or is an irreducible element of R or  = 0. = 0.
Proof: Let P be a prime ideal of R. Assume that P  (0). Since P is a nontrivial ideal of R, P = (a) for a (0). Since P is a nontrivial ideal of R, P = (a) for a  Rx, where a is a nonunit. Since R is a PID, R is a UFD, so we may write a = Rx, where a is a nonunit. Since R is a PID, R is a UFD, so we may write a =  1... 1... r, where r, where  i is an irreducible element of R. Suppose that r > 2. Set b = i is an irreducible element of R. Suppose that r > 2. Set b =  1, c = 1, c =  2... 2... r. Then bc r. Then bc  P. Moreover, b P. Moreover, b 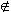 P and c P and c 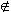 P. (For example, if b P. (For example, if b  P, then b = da for some d P, then b = da for some d  R, so that 1 = dc, and thus c is a unit, which is a contradiction.) This contradicts the assumption that P is prime. Thus, r = 1 and P = ( R, so that 1 = dc, and thus c is a unit, which is a contradiction.) This contradicts the assumption that P is prime. Thus, r = 1 and P = ( 1). On the other hand, if P = ( 1). On the other hand, if P = ( ), where ), where  is irreducible, then P is prime by Example 2. The ideal (0) is prime since a · b is irreducible, then P is prime by Example 2. The ideal (0) is prime since a · b  (0), then either a = 0 or b = 0 since R is an integral domain. (0), then either a = 0 or b = 0 since R is an integral domain.
Theorem 3: Let P be an ideal of R, a commutative ring with identity, P  (1). Then P is a prime ideal if and only if R/P is an integral domain. (1). Then P is a prime ideal if and only if R/P is an integral domain.
Proof:  Assume that P is a prime ideal. It is clear that R/P is a commutative ring with identity. To show that R/P is an integral domain, we must show that if a + P, b + P Assume that P is a prime ideal. It is clear that R/P is a commutative ring with identity. To show that R/P is an integral domain, we must show that if a + P, b + P  R/P are such that (a + P)(b + P) = 0 + P, then either a + P = 0 + p b + P = 0 + P. But (a + P)(b + P) = ab + P, so that if (a + P)(b + P) = 0 + P ab R/P are such that (a + P)(b + P) = 0 + P, then either a + P = 0 + p b + P = 0 + P. But (a + P)(b + P) = ab + P, so that if (a + P)(b + P) = 0 + P ab  P. Therefore, since P is a prime ideal, either a P. Therefore, since P is a prime ideal, either a  P of b P of b  P. Thus either a + P or b + P equals 0 + P. P. Thus either a + P or b + P equals 0 + P.
 Assume that R/P is an integral domain and that a,b Assume that R/P is an integral domain and that a,b  R, are such that ab R, are such that ab  P. Then P. Then
(a + P)(b + P) = ab + P
= 0 + P
Therefore, since R/P is an integral domain, either a + P or b + P equals 0 + P. Hence either a  P or b P or b  P. P.
Corollary 4: Let F be a field, and let X and Y be indeterminates over F. Then (X,Y) is a prime ideal of F[X,Y].
Proof: Consider the homomorphism
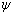 : F[X,Y]  F
defined by mapping f into its value at (0,0). It is easy to see that 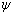 is surjective and ker( is surjective and ker(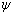 = (X,Y). Therefore, F[X,Y]/(X,Y) = (X,Y). Therefore, F[X,Y]/(X,Y)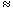 F. But F is an integral domain, so that (X,Y) is a prime ideal by Theorem 3. F. But F is an integral domain, so that (X,Y) is a prime ideal by Theorem 3.
If R is a PID, we can rephrase the unique factorization in R in terms of prime ideals. This was the original motivation for introducing prime ideals into mathematics.
Theorem 5: Let R be a principal ideal domain, A an ideal of R, A (0) or (1). Then A can be written as a product of prime ideals of R, and this expression is unique up to reordering of the prime ideals concerned. (0) or (1). Then A can be written as a product of prime ideals of R, and this expression is unique up to reordering of the prime ideals concerned.
Proof: Let A = (a). Then, since A  (0),(1), we see that a (0),(1), we see that a 0 or a unit of R. Therefore, since R is a UFD, we may write 0 or a unit of R. Therefore, since R is a UFD, we may write
a =  1 1...  s s,
 i (1 < i < s) irreducible. but then i (1 < i < s) irreducible. but then
A = (a) =(  i i)...(  s s)
is an expression of A as a product of prime ideals ( 1),...,( 1),...,( s). Suppose that s). Suppose that
A = (  1 1)...(  s s)
= (  ' 1)...(  ' t).
[Every nonzero prime ideal of R is of the form ( ) for ) for  irreducible.] Then irreducible.] Then
where  is a unit of R. But since R is a UFD, s = t and we may renumber is a unit of R. But since R is a UFD, s = t and we may renumber  1,..., 1,..., s so that s so that  i and i and  'i are associates (1 < i < s). then ( 'i are associates (1 < i < s). then ( i) = ( i) = ( 'i) and the two decompositions of (1) are the same except for the order of the prime ideals. 'i) and the two decompositions of (1) are the same except for the order of the prime ideals.
We have seen that there exist fairly simple integral domains (such as Z[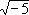 ]) for which unique factorization does not hold. However, it makes sense to inquire whether every nontrivial ideal of such a ring can be written uniquely as a product of prime ideals, where uniqueness is taken to mean up to rearrangement. In essence, this is Kummer's idea. It is easy to see that if unique factorization among ideals holds and if the ring is a UFD, then the ring is a PID. Thus, in the case of all ideals are principal, unique factorization of ideals and unique factorization of elements are equivalent. However, if there exist nonprincipal ideals, then it is possible for unique factorization of ideals to hold even though unique factorization of elements does not. An integral domain in which every nontrivial ideal can be expressed uniquely as a product of prime ideals is called a Dedekind domain. The rings Z[ ]) for which unique factorization does not hold. However, it makes sense to inquire whether every nontrivial ideal of such a ring can be written uniquely as a product of prime ideals, where uniqueness is taken to mean up to rearrangement. In essence, this is Kummer's idea. It is easy to see that if unique factorization among ideals holds and if the ring is a UFD, then the ring is a PID. Thus, in the case of all ideals are principal, unique factorization of ideals and unique factorization of elements are equivalent. However, if there exist nonprincipal ideals, then it is possible for unique factorization of ideals to hold even though unique factorization of elements does not. An integral domain in which every nontrivial ideal can be expressed uniquely as a product of prime ideals is called a Dedekind domain. The rings Z[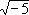 ] and Z[ ] and Z[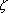 ] are examples of Dedekind domains. ] are examples of Dedekind domains.
Having introduced the prime ideals of a ring, let us now introduce another important class of ideals - the maximal ideals. An ideal A of R is said to be proper if A R. R.
Definition 6: An ideal M of R is said to be a maximal ideal if (a) M is a proper ideal and (b) if A is a proper ideal containing M, then M = A.
We can reformulate the definition of a maximal ideal in a more convenient way:
Lemma 7: Let M be a proper ideal of R. Then if M is a maximal ideal for all x  R - M. we have M + (x) = R. R - M. we have M + (x) = R.
Proof:  Let x Let x  R - M. Then A = M + (x) is an ideal containing M. If A is proper, then M = A, since M is maximal. But this is impossible, since x R - M. Then A = M + (x) is an ideal containing M. If A is proper, then M = A, since M is maximal. But this is impossible, since x  A - M. Therefore, M + (x) = R. A - M. Therefore, M + (x) = R.
 Let A be a proper ideal containing M, and let x Let A be a proper ideal containing M, and let x  A - M. Then M + (x) = R. Thus, A = R, which is a contradiction to the assumption that A is proper. But this implies that A - M = A - M. Then M + (x) = R. Thus, A = R, which is a contradiction to the assumption that A is proper. But this implies that A - M =  and M and M  A. Therefore, since M A. Therefore, since M A, we have M = A and M is maximal. A, we have M = A and M is maximal.
Example 5: Let R be a PID,  an irreducible element of R. then ( an irreducible element of R. then ( ) is a maximal ideal. For if x ) is a maximal ideal. For if x  R-( R-( ), then x is not divisible by ), then x is not divisible by  . Thus, since . Thus, since  is irreducible, x and is irreducible, x and  are relatively prime. So there exist a,b are relatively prime. So there exist a,b  R such that a R such that a + bx = 1. Thus, 1 + bx = 1. Thus, 1  ( ( ) + (x), and ) + (x), and
(  ) + (x) = (1) = R,
so that ( ) is a maximal ideal. In particular, if p is prime, then (p) is a maximal ideal of Z, and if f ) is a maximal ideal. In particular, if p is prime, then (p) is a maximal ideal of Z, and if f  F[X] is irreducible, then (f ) is a maximal ideal of F[X]. F[X] is irreducible, then (f ) is a maximal ideal of F[X].
Theorem 8: M is a maximal ideal of R if and only if R/M is a field.
Proof:  Assume that M is maximal. Then M is proper, so that R/M is not the trivial ring. Let x + M Assume that M is maximal. Then M is proper, so that R/M is not the trivial ring. Let x + M  R/M, x + M R/M, x + M  0 + M. We must show that x + M is a unit in R/M. But x 0 + M. We must show that x + M is a unit in R/M. But x  M, so that by Lemma 7, M + (x) = R. In particular, 1 M, so that by Lemma 7, M + (x) = R. In particular, 1  M + (x), so that there exists a M + (x), so that there exists a  R such that 1 - ax R such that 1 - ax  M. But then (a + M)(x + M) = 1 + M and x + M is a unit in R/M. M. But then (a + M)(x + M) = 1 + M and x + M is a unit in R/M.
 Assume that R/M is a field. Then R/M is not the trivial ring, so that R/M Assume that R/M is a field. Then R/M is not the trivial ring, so that R/M {M} and M is proper. Let x {M} and M is proper. Let x  R - M. Then x + M R - M. Then x + M  0 + M, so that there exists a + M 0 + M, so that there exists a + M  R/M such that (a + M)(x + M) = 1 + M. But then 1 - ax R/M such that (a + M)(x + M) = 1 + M. But then 1 - ax  M and 1 M and 1  (x) + M, so that M + (x) = R. Thus, M is maximal by Lemma 7. (x) + M, so that M + (x) = R. Thus, M is maximal by Lemma 7.
Corollary 9: If M is a maximal ideal, then M is a prime ideal.
Proof: If M is maximal, then R/M is a field by Theorem 8. But a field is an integral domain, so that M is prime by Theorem 3.
We have seen that every maximal ideal is a prime. However, the converse is not true. For example, let R = F[X,Y]. Then (X) is a prime ideal since X is irreducible in R. However, (X) is not a maximal ideal since (X)  (X,Y) (X,Y)  R and (X,Y) is a proper ideal such that (X,Y) R and (X,Y) is a proper ideal such that (X,Y)  (X). (X).
A maximal ideal cannot be properly contained in any nontrivial ideal. Thus it is natural to ask if every ideal which is not the entire ring is contained in some maximal ideal. This is a highly nontrivial question. Consider the following example. Let C[0,1] denote the set of all continuous real-valued functions on the closed interval [0,1], and let sum and product of functions be defined in the usual way, so that C[0,1] becomes a commutative ring with identity. For each integer j(j = 1,2,3,...) let Ij = X1/2jC[0,1]. Then Ij is a principal ideal and
I j I 2  ...
Therefore, it is clear that none of the Ij is a maximal ideal. Is there a maximal ideal containing Ij? It is not obvious, but in fact there is. For let I denote the set of all functions in C[0,1] which are zero at x = 0. Then it is easy to see that I is an ideal of C[0,1]. Moreover, I is a maximal ideal, being the kernel of the surjective homomorphism
C[0,1]  R R,
f  f f(0).
Thus since R is a field, I is a maximal ideal by Theorem 8. And it is clear that I contains all the ideals Ij.
Theorem 10: Let I be a proper ideal of the commutative ring with identity R. Then I is contained in some maximal ideal of R.
The proof of Theorem 10 will not be given since it rests on a very subtle set-theoretic result known as Zorn's lemma, which in turn is a consequence of the axiom of choice, a set theory axiom which is very convenient to assume and which has actually entered into a number of proofs in this presentation.
|
 B
B B
B A
A B
B B
B A
A H
H G
G H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
Let M be a proper ideal of R. Then if M is a maximal ideal for all
G | f(x) = 1H}.
Let M be a proper ideal of R. Then if M is a maximal ideal for all  R - M.
R - M. (1).
(1). R
R P
P P or
P or  P.
P.

 R,
R, irreducible. If
irreducible. If  |ab,
|ab, |a
|a |b.
|b. Rx
Rx Rx
Rx 1 ...
1 ...  s =
s = 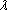 1 ...
1 ... 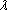 t
t 1 ...
1 ...  s
s 1 and
1 and 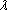 1 are associates
1 are associates  I,
I, R,
R, I
I I.
I.
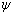 : F[X,Y]
: F[X,Y]  F
F 1...
1... s,
s, i)...(
i)...( s)
s) 1)...(
1)...( s)
s) '1)...(
'1)...( 't).
't).
 1...
1... s) = (
s) = ( '1...
'1... 't)
't)
 1...
1... s =
s = 
 '1...
'1... 't.
't. ) + (x) = (1) = R,
) + (x) = (1) = R, I2
I2  ...
... R,
R, f(0).
f(0).